2. Специфичность закономерности расселения

Теперь мы подготовленны к тому, чтобы понять, что могут существовать, если не теоретические, то эмпирические формулы, которые достаточно верно передают ход кривых расселения, рассмотренных выше, в зависимости от тех параметров, которые – с точки зрения рассмотренных оснований – влияют на расселение.

Но прежде, чем показать, что такое правило действительно может быть указано, следует убедиться, что обнаруженные правильности расселения нельзя объяснять простой случайностью. Последняя, как известно, имеет свои законы. И применяя их к данным обстоятельствам, можно показать, что если действительно расселение определяется чистым случаем, то на расстояние от 0 до r, если расселение вообще возможно от 0 до R, поселится следующее число жителей , (1)

где θ есть символ известной к теории вероятностей функции.

Действительно, предположим, что расселение не подчиняется какой-либо ему свойственной закономерности, а случайно, другими словами, определяется законами случая. Количество живущих n на некотором выраженном во времени расстоянии t от места их постоянного тяготения обозначим через n=f(t) (2)

причем n условимся определять в долях единицы. В таком случае n будет вероятностью расселения на расстоянии t.

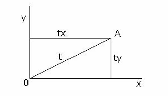Эту вероятность иначе можно выразить, как вероятность совместного события, что точка А будет на расстояниях во времени t_x и t_y соответственно от осей y и x.

Таким образом, n=f(t)=f(t_x)*f(t_y) (3)

но, как известно, существует единственная функция; отвечающая условию (3). Эта функция будет следующей:

n=f(t)= (4)

Вероятность расселения в интервале расстояний от t₁ до t₂ будет:

(5)

Выражение (5) и является исходным для решения поставленной выше задачи.

В этих целях сведём выражение 1 к известной в исчислении вероятностей функции

(6)

а вычисление поведем, начиная от расстояния t₁ = 0.

Полагая ct = u, будем иметь:

Итак, (7)

Так как достоверно, что расселение происходит полностью в пределах расстояний от 0 до , то

т.к. =1.

Итак, коэффициенты “a” и “c” в выражении (5) или (7), связаны зависимостью

=1

и выражение (7) упрощается : (9)

Заменим теперь время t через расстояние r и скорость транспорта v. Тогда

Произвольная постоянная С определяется из предельного условия.

Функция , как известно, чрезвычайно быстро приближается к 1 с ростом её аргумента:

(2) = 0,9953; (3) = 0,9999779; (4)=0,999999984… (10)

Поэтому вероятностьбудет практически равна 1 при значениях аргумента выражения (9), начиная от 3 или 4.

Выбор этого предельного значения аргумента выражения (9) зависит от размера населения города. Принимая за предельное значение аргумента 3, возможный просчет для города в 100 тыс.человек, следуя (10), будет всего в 3 чел. и в 22 чел. для миллионного города. Поэтому 3, как предельное значение аргумента, дает совершенно достаточную точность.

Но с другой стороны , следуя зависимости (9), приближается к 1 с ростом r. Если поэтому мы примем установочное предельное условие, что расселение заканчивается на расстоянии не большем R, то С и R связаны зависимостью

или (11)

Поэтому окончательно имеем:

Функция (11) и положена в основу расчета кривой распределения пассажиров по дальности поездок для случая, приводимого Зильберталем и рассмотренного выше, когда R = 12 км.

Следуя этой кривой расселения и рассуждая обратно тому, как мы рассуждали выше, можно по этой кривой построить кривую распределения пассажиров для случая Зильберталя (см. рис.5), взятого для ленинградского трамвая. Для этого достаточно в формуле (1) R положить 12 км. Рис.8 показывает результат такого построения: кривая фактического распределения весьма несходна с теоретической кривой, построенной на гипотезе случайного расселения.

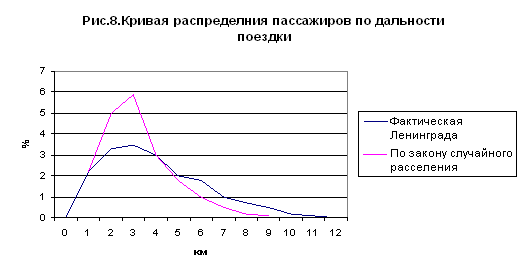
Это и требовалось доказать: расселение не случайно, и, следовательно, должна существовать иная характерная для расселения закономерность.